Zbrajanje i oduzimanje razlomaka: Vodič za učenike
Razlomci mogu djelovati zastrašujuće, ali uz pravi pristup i vizualizaciju, postaju jednostavni! U ovom članku naučit ćeš kako zbrajati i oduzimati razlomke korak po korak.
📚 Dio 1: Zbrajanje razlomaka
Zbrajanje razlomaka s istim nazivnikom
Kada razlomci imaju isti nazivnik, zbrajanje je jednostavno – samo zbrojiš brojnike, a nazivnik ostaje isti.
Objašnjenje 1: Koliko je ?
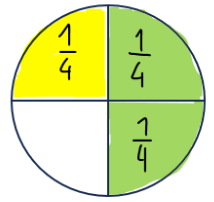
Zamislimo pizzu podijeljenu na 4 jednaka dijela.
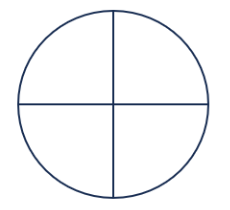
Korak 1: Vizualno prikažimo razlomak. Nacrtamo krug i podijelimo ga na 4 dijela.
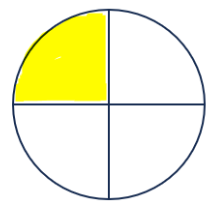
Korak 2: Prvo ćemo obojiti jednu kruga (prvi komad pizze).
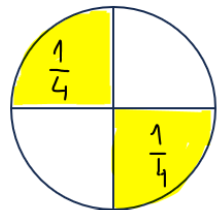
Korak 3: Zatim ćemo obojiti drugu kruga (drugi komad pizze).
Korak 4: Sada ćemo zbrojiti . Samo po slici možemo vidjeti da smo pojeli pizze.
Dakle, ako pojedem pizze, a zatim pojedem još pizze, pojela sam pizze. Iz ekvivalentnih razlomaka znamo da možemo skratiti s 2 i to je .
💡 Zapamti: Kada su nazivnici isti, samo zbrajamo brojnike!
Objašnjenje 2: Koliko je ?
Korak 1: Provjeravamo jesu li nazivnici isti. Oba nazivnika su 5 ✓
Korak 2: Ako su nazivnici isti, nazivnik prepišemo. Samo zbrajamo brojnike: 2 + 1 = 3
Korak 3: Rezultat je .
Zbrajanje razlomaka s različitim nazivnicima
Kada razlomci imaju različite nazivnike, moramo ih prvo svesti na zajednički nazivnik.
Objašnjenje 3: Koliko je ?
Korak 1: Vratimo se na primjer pizze. Pizzu podijelimo na 4 jednaka dijela.
Korak 2: Prvo obojimo pizze.
Korak 3: Zatim obojimo još pizze. Ali pazi! pizze je isto što i pizze.
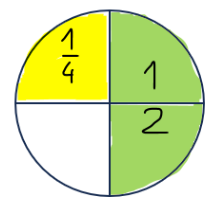
Korak 4: Zbrajamo razlomke:
Dakle, pojeli smo pizze.
Objašnjenje 4: Koliko je ?
Ovo je malo složeniji primjer jer nazivnici (2 i 3) nemaju očitu vezu.
Korak 1: Oba nazivnika trebaju biti ista da ih možemo zbrojiti. Da bismo ih sveli na zajednički nazivnik, moramo pronaći najmanji zajednički višekratnik (NZV) brojeva 2 i 3.
Korak 2: Razlomke ćemo svesti na zajednički nazivnik 6.
Prvo ćemo zapisati kao šestine:
- U nazivniku pišemo 6
- Da bismo dobili brojnik: , zatim
Ponovimo postupak za :
- U nazivniku pišemo 6
- Da bismo dobili brojnik: , zatim
Korak 3: Zbrajanje razlomaka:
📚 Dio 2: Oduzimanje razlomaka
Oduzimanje razlomaka je jako slično zbrajanju razlomaka – samo umjesto zbrajanja brojnika, oduzimamo ih!
Oduzimanje razlomaka s istim nazivnikom
Objašnjenje 1: Koliko je ?
Korak 1: Provjeravamo nazivnike. Ako imamo isti nazivnik, nazivnik u razlici bit će isti kao i nazivnici u dva broja koja oduzimamo.
Dakle, 18 je u oba i pišemo 18.
Korak 2: U brojnik ćemo upisati razliku između dva brojnika:
Korak 3: Odgovor je .
Ali čekaj! Odgovor nije pojednostavljen jer su i 3 i 18 djeljivi s 3.
Rezultat:
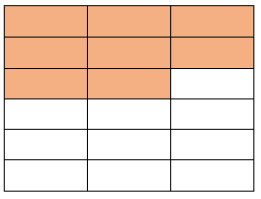
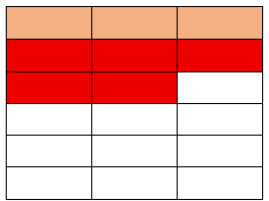
Prikazat ćemo vizualno
Oduzimanje
Oduzmi od .
Kada pretvorimo u jedan komad.
Koliko komada imamo?
=
Oduzimanje razlomaka s različitim nazivnicima
Objašnjenje 2: Koliko je ?
Korak 1: Imamo razlomke s različitim nazivnicima. Ključno je zapisati razlomke s različitim nazivnicima u razlomke s istim nazivnicima.
Zajednički nazivnik će biti zajednički višekratnik brojeva 3 i 5.
Korak 2: Počet ćemo s većim brojem, a to je 5. Prođimo kroz njegove višekratnike:
- 5 nije djeljiv s 3 ✗
- 10 nije djeljiv s 3 ✗
- 15 je djeljiv s 3 ✓
Zajednički nazivnik je 15.
Korak 3: Zapisat ćemo kao razlomak s nazivnikom 15:
Korak 4: Ponovit ćemo postupak s razlomkom :
Korak 5: Sada jednostavno oduzimamo brojnike, a nazivnik prepišemo:
Možemo ga zapisati kao mješoviti broj:
Objašnjenje 3: Koliko je ?
Korak 1: Imamo različite nazivnike (10 i 8) i potrebno je pronaći zajednički nazivnik.
Korak 2: Pretvorimo razlomke na zajednički nazivnik 40:
Korak 3: Oduzimamo:
🎯 Sažetak pravila
| Situacija | Što radimo? |
|---|---|
| Isti nazivnici | Zbrajamo/oduzimamo samo brojnike, nazivnik ostaje isti |
| Različiti nazivnici | Prvo pronađemo NZV, svedemo na zajednički nazivnik, pa zbrajamo/oduzimamo |
| Rezultat se može skratiti | Uvijek skrati razlomak na najmanji oblik! |
📝 Zadaci za vježbu
Zadatak 1
Izračunaj:
a)
b)
✅ Rješenja
Zadatak 1a:
Korak 1: Pronađemo
Korak 2: Svedemo na zajednički nazivnik:
Korak 3: Računamo:
Rezultat:
Zadatak 1b:
Korak 1: Pronađemo
Korak 2: Svedemo na zajednički nazivnik:
Korak 3: Računamo:
Rezultat:
💡 Savjeti za uspjeh
- Uvijek provjeri nazivnike – jesu li isti ili različiti?
- Pronađi NZV – najmanji broj koji je djeljiv s oba nazivnika
- Ne zaboravi skratiti – uvijek pojednostavi rezultat
- Vizualiziraj – nacrtaj pizzu ili čokoladu ako ti pomaže!
- Provjeri rezultat – uvrsti natrag i vidi ima li smisla
Sretno s vježbanjem! 🍕