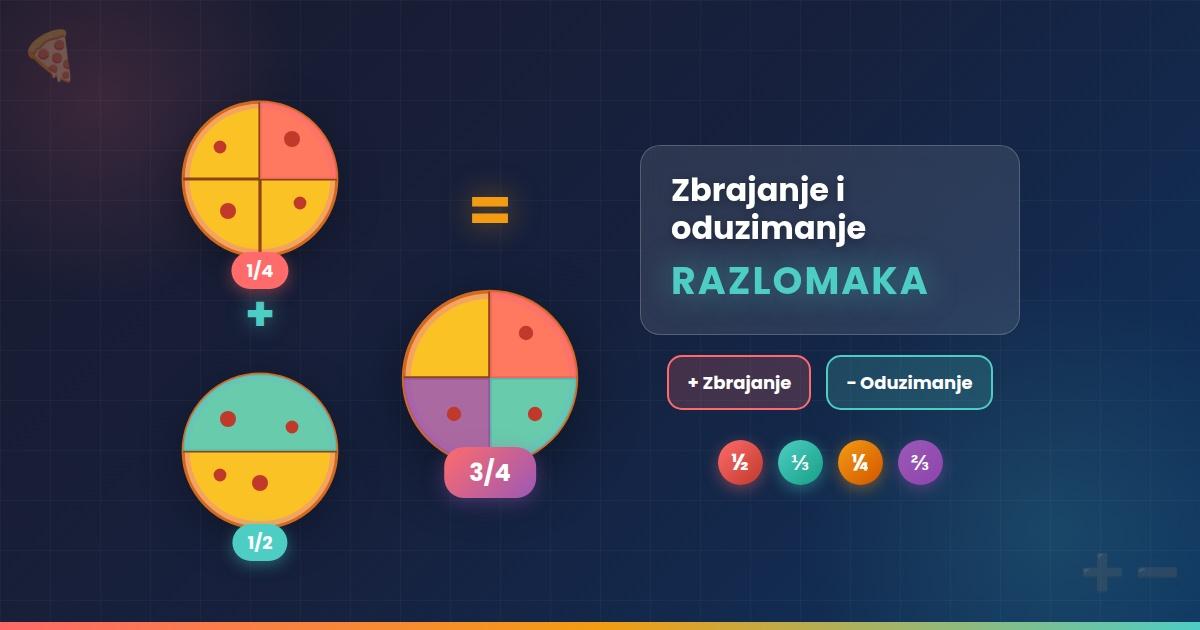
Mješoviti brojevi

Dosad smo naučili kako obojiti ½ ili ⅘. Međutim, možemo obojiti i 5/3, 4/2, 6/4... Upoznat ćemo razlomke u kojima je brojnik veći od nazivnika.

---

Objašnjenje 1

Oboji 4/3 pravokutnika.

Nazivnik 3 govori nam da ovdje imamo trećine, tj. da pravokutnik trebamo podijeliti na tri jednaka dijela.

Brojnik 4 govori nam da trebamo obojiti četiri takva dijela. Kako obojiti četiri ako ih imamo samo tri?

Postupak

Prvo obojimo sve dijelove koje imamo (dakle, sva tri), a nakon toga docrtamo još jedan isti takav pravokutnik, napravimo istu podjelu (dakle, opet na trećine) te obojimo još jednu trećinu. Time će biti obojene četiri trećine pravokutnika.

$\frac{4}{3} = 1\frac{1}{3}$

Zapamti: Kada je brojnik veći od nazivnika, imamo nepravi razlomak. Takav razlomak možemo zapisati kao mješoviti broj.

---

Objašnjenje 2

Koliki je dio lika obojen? Izrazi razlomkom.

Korak 1

Broji cijele dijelove.

Imamo ih ukupno tri.

Korak 2

Pronađi razlomak.

Imamo 10 jednakih dijelova. 9 dijelova je obojeno.

Razlomak je 9/10.

Zaključak

Mješoviti broj je $3\frac{9}{10}$.

Čitamo ga kao "tri cijela i devet desetina".

---

Zadatak 1

Koliki je dio lika obojen? Izrazi razlomkom.

a)

b)

c)

d)

e)

f)

---

Promjena zapisa - nepravi razlomak, mješoviti i prirodni broj

Budući da za svaki nepravi razlomak vrijedi da je on veći od broja 1, on se može zapisati ili kao mješoviti ili kao prirodni broj.

---

Nepravi razlomak u mješoviti broj

Objašnjenje 1

Napiši $3\frac{1}{3}$ kao nepravi razlomak.

Da biste zapisali $3\frac{1}{3}$ kao nepravi razlomak, prvo pronađite razlomak koji je ekvivalentan broju 3. Budući da ⅓ ima nazivnik 3, ovaj razlomak također bi trebao imati nazivnik 3.

$3 = \frac{9}{3}$

Sada zapiši $3\frac{1}{3}$ kao zbroj razlomaka.

$3\frac{1}{3} = \frac{9}{3} + \frac{1}{3} = \frac{10}{3}$

Dakle, $3\frac{1}{3}$ možete zapisati kao nepravi razlomak $\frac{10}{3}$.

---

Objašnjenje 2

Mješoviti broj možemo napisati kao nepravi razlomak i na drugi način.

Mješoviti broj $2\frac{1}{3}$ zapiši kao nepravi razlomak.

Postupak

Korak 1: Pomnoži cijeli broj s nazivnikom.

$2 \times 3 = 6$

Korak 2: Dodaj brojnik.

$6 + 1 = 7$

Korak 3: Napiši rezultat kao brojnik, a nazivnik ostaje isti.

$2\frac{1}{3} = \frac{7}{3}$

Formula: $a\frac{b}{c} = \frac{a \times c + b}{c}$

---

Zadatak 2

Mješoviti broj zapiši kao nepravi razlomak.

1. $4\frac{3}{7}$ = ___

2. $8\frac{5}{11}$ = ___

3. $9\frac{1}{6}$ = ___

4. $12\frac{5}{8}$ = ___

5. $4\frac{7}{9}$ = ___

6. $6\frac{2}{5}$ = ___

7. $2\frac{1}{7}$ = ___

8. $1\frac{7}{8}$ = ___

---

Mješoviti broj u razlomak

Objašnjenje 1

Zapiši $\frac{19}{2}$ kao mješoviti broj.

Najlakši način da pretvorimo razlomak u mješoviti broj je dijeljenje 19 sa 2.

$19 : 2 = 9 \text{ (ostatak 1)}$

Dobili smo 9 cijelih i ostatak 1.

To zapisujemo kao $9\frac{1}{2}$.

Zapamti: Ostatak ide u brojnik, a nazivnik ostaje isti.

---

Zadatak 3

Na isti način riješi ove primjere.

1. $\frac{7}{4}$ = ___

2. $\frac{13}{3}$ = ___

3. $\frac{11}{5}$ = ___

4. $\frac{5}{6}$ = ___

5. $\frac{8}{4}$ = ___

6. $\frac{9}{4}$ = ___

7. $\frac{23}{23}$ = ___

---

Sažetak

Pojam	Opis	Primjer
Pravi razlomak	Brojnik < nazivnik	$\frac{2}{3}$
Nepravi razlomak	Brojnik ≥ nazivnik	$\frac{5}{3}$
Mješoviti broj	Cijeli broj + razlomak	$1\frac{2}{3}$

Pretvorba mješovitog broja u nepravi razlomak:

$a\frac{b}{c} = \frac{a \times c + b}{c}$

Pretvorba nepravog razlomka u mješoviti broj:

Dijeli brojnik s nazivnikom. Količnik je cijeli broj, a ostatak je novi brojnik.

---

Rješenja

Zadatak 2

1. $4\frac{3}{7} = \frac{31}{7}$

2. $8\frac{5}{11} = \frac{93}{11}$

3. $9\frac{1}{6} = \frac{55}{6}$

4. $12\frac{5}{8} = \frac{101}{8}$

5. $4\frac{7}{9} = \frac{43}{9}$

6. $6\frac{2}{5} = \frac{32}{5}$

7. $2\frac{1}{7} = \frac{15}{7}$

8. $1\frac{7}{8} = \frac{15}{8}$

Zadatak 3

1. $\frac{7}{4} = 1\frac{3}{4}$

2. $\frac{13}{3} = 4\frac{1}{3}$

3. $\frac{11}{5} = 2\frac{1}{5}$

4. $\frac{5}{6}$ = pravi razlomak (ne može se pretvoriti)

5. $\frac{8}{4} = 2$

6. $\frac{9}{4} = 2\frac{1}{4}$

7. $\frac{23}{23} = 1$